动态规划

背包问题

犹记得大三上算法设计这门课时，动态规划给我印象最深的经典问题就是最长公共子序列(LCS)和背包问题

背包问题是一种组合优化的NP完全问题：

有$N$个物品和容量为$W$的背包，每个物品都有自己的体积$w$和价值$v$，如何分配使得背包所装下物品的总价值最大?

通用的动规划分为：

• 设 $dp[i][j]$ 表示前 $i$ 件物品的总体积不超过 $j$ 的情况下，背包里物品能达到的最大价值

按每个物品可以被拿取的数量进行分类，进一步可分为0-1背包和完全背包两种，状态转移方程也不同

0-1背包问题

限定每种物品只能选择0个或1个(要么不拿要么拿)

分析一下子问题的状态转移(当遍历到第 $i$ 件物品时)：

• 在当前背包容量为 $j$ 的情况下，如果放不下重量为 $w_i$ 的物品 $i$，则前 $i$ 件物品的最大价值只能取前 $i-1$ 件物品的最大价值：$dp[i][j] = dp[i-1][j]$

• 如果物品 $i$ 能放入背包中，则前 $i$ 件物品的最大价值就能更新为以下两种情况的最大值：

  1. 在背包容量为 $j - w_i$ 的情况下前 $i-1$ 件物品的最大价值 加上 物品 $i$ 的价值 $v$：$dp[i-1][j-w_i]+v$

  2. 不拿物品 $i$ ，就是以背包容量 $j$ 装下前 $i-1$ 件物品的最大价值：$dp[i-1][j]$

  最后状态转移分支为 $dp[i][j] = \max(dp[i-1][j], dp[i-1][j-w_i] + v)$

以 $i = 2$ 为例，物品 $2$ 的重量 $w = 2$、价值$v = 3$，遍历到背包容量为 $j’$ 时需要上一行的2个信息$dp[1][j’]$ 和 $dp[1][j’-2]$，状态转移矩阵如下图所示

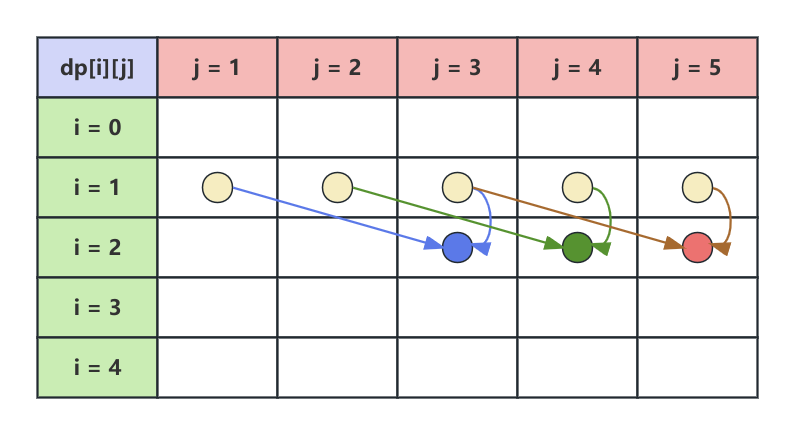
整个状态转移方程为：

dp数组每个位置的初始值都应为0，且更新dp数组需要两趟遍历，对背包的每个可装物品数 $i \in [1, N]$ 都要遍历一次不同背包容量 $j \in [1, W]$ 情况下的最大值子问题，时间复杂度和空间复杂度都为 $O(NW)$

int backpack_zero_one(vector<int> weights, vector<int> values, int N, int W) {
    vector<vector<int>> dp(N + 1, vector<int>(W + 1, 0));
    for (int i = 1; i <= N; i++) {
        int w = weights[i-1], v = values[i-1];
        for (int j = 1; j <= W; j++) {
            if (j >= w)
                dp[i][j] = max(dp[i-1][j], dp[i-1][j-w] + v);
            else
                dp[i][j] = dp[i-1][j];
        }
    }
    return dp[N][W];
}

空间压缩优化

观察状态转移矩阵可以发现，每一趟 $i$ 实际都只用到了其上一趟 $i-1$ 的dp子问题，前面几趟的计算结果实际上都不会被使用，所以可以去掉表示物品个数 $i$ 的维度，仅用 $dp[j]$ 表示背包容量为 $j$ 时能够得到的最大价值，且只需要计算背包容量 $j$ 不小于当前物品 $i$ 的重量 $w_i$ 的情况（否则 $dp[j]$ 保持为上一趟的值即可）：

注意：在遍历 $j$ 的时候，需要从最大背包容量 $W$ 开始向当前物品 $i$ 的体积 $w_i$ 逆向遍历，因为扫描完上一行 $i - 1$ 的物品数时，$dp[j - w_{i-1}]$存储的是上一趟的子问题，如果 $j$ 从当前的 $w_i$ 开始遍历，某个 $j’$ 时要读取的$dp[j’-w_{i-1}]$已经被更新为$dp[j-w_i]$了，就无法获取到上一趟子问题的解

int backpack_zero_one(vector<int> weights, vector<int> values, int N, int W) {
    vector<int> dp(W + 1, 0);
    for (int i = 1; i <= N; i++) {
        int w = weights[i-1], v = values[i-1];
        for (int j = W; j >= w; j--)    // 逆向遍历
            dp[j] = max(dp[j], dp[j-w] + v);
    }
    return dp[W];
}

完全背包问题

限定每种物品可以拿任意次

因为物品可以拿任意多次，所以遍历到物品 $i$ 时不仅要考虑用之前容量为 $j - w$ 的背包再加1个物品 $i$，还要考虑丢掉背包其他物品装更多的物品 $i$ 的情况，比如 $j - 2w$、$j - 3w$ 等

如果照这样写出状态转移方程，当背包容量趋于$+\infty$而物体体积趋于$0$，这样更新dp数组时的比较次数也趋于$+\infty$，远超0-1背包问题的 $O(NW)$ 的复杂度

其实可以从状态转移矩阵进行分析：以 $dp[2][5]$ 为例，假设物品 $2$的体积 $w=2$、价值 $v=3$，由于当前背包容量 $j=5$，最多只能装下2个该物品，则状态转移方程为 $dp[2][5]=\max(dp[1][5], dp[1][3] + 1 \times 3, dp[1][1] + 2 \times 3)$，如下图所示

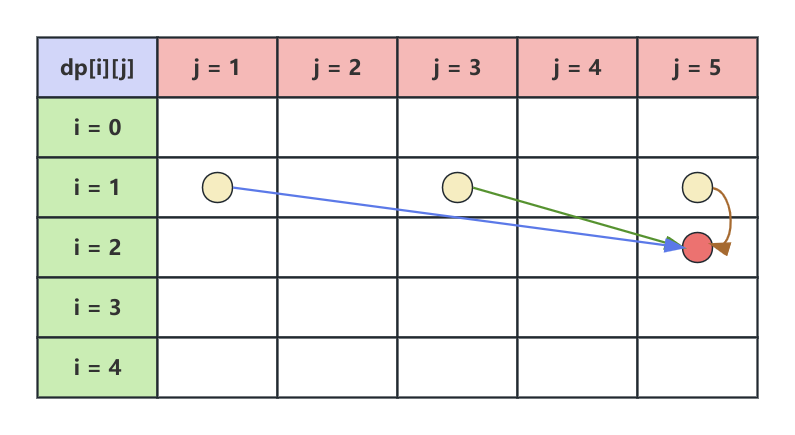
观察状态转移矩阵，由于在更新 $dp$ 矩阵的时候是固定 $i$，然后从 $j = 1$ 开始逐步扫描到 $j = W$，所以获取上一行的 $dp[1][1]$ 和 $dp[1][3]$ 的时候，可以发现：

• 计算 $dp[2][1]$ 时已经考虑过 $dp[1][1]$

• 计算 $dp[2][3]$ 时已经考虑过 $dp[2][1]$ 和 $dp[1][3]$

所以对于 $dp[2][5]$ 而言，只需要考虑 $dp[2][3]$ 和 上一行的$dp[1][5]$ 即可：$dp[2][5]=\max(dp[1][5], dp[2][3] + 3)$，如下图所示

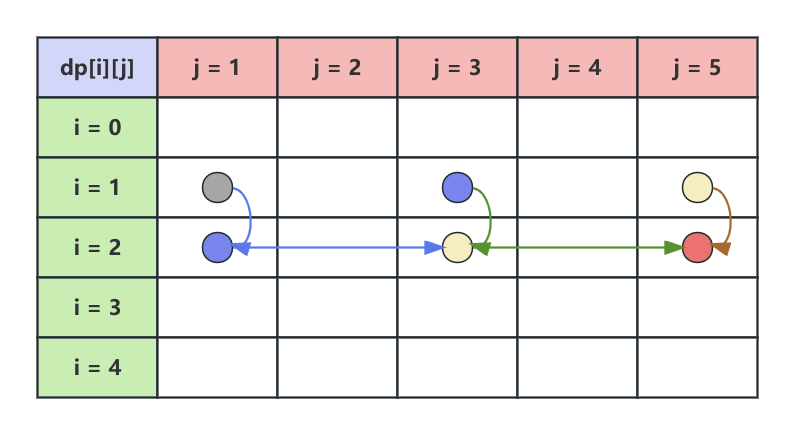
所以最终的状态转移方程为：

完全背包的状态转移方程与0-1背包的差别只是将 $dp[i-1][j-w]$ 变成了 $dp[i][j-w]$

int backpack_complete(vector<int> weights, vector<int> values, int N, int W) {
    vector<vector<int>> dp(N + 1, vector<int>(M + 1, 0));
    for (int i = 1; i <= N; i++) {
        int w = weights[i], v = values[i];
        for (int j = 1; j <= W; j++) {
            if (j >= w)
                dp[i][j] = max(dp[i-1][j], dp[i][j-w] + v);
            else
                dp[i][j] = dp[i-1][j];
        }
    }
    return dp[N][W];
}

空间压缩优化

与0-1背包一样，完全背包的状态转移方程也仅依赖上一行的信息，因此也可以将空间复杂度降低到 $O(W)$，但是需要注意的是：

• 0-1背包空间压缩后由于需要上一趟的信息，只能逆序遍历

• 完全背包的状态转移方程需要上一行当前列的信息 $dp[i-1][j]$ (压缩后存储在 $dp[j]$ 中) 和 同一行先行列的信息 $dp[i][j-w]$ (压缩后存储在 $dp[j-w]$ 中)

所以完全背包进行空间压缩后，必须从 $j = w$ 开始正向遍历到 $j = W$，因为需要当前物品 $i$ 在 第 $j - w$ 列的信息

int backpack_complete(vector<int> weights, vector<int> values, int N, int W) {
    vector<int> dp(W + 1, 0);
    for (int i = 1; i <= N; i++) {
        int w = weights[i-1], v = values[i-1];
        for (int j = w; j <= W; j++)    // 正向遍历
            dp[j] = max(dp[j], dp[j-w] + v);
    }
    return dp[W];
}

• ← Previous Post
• Next Post →